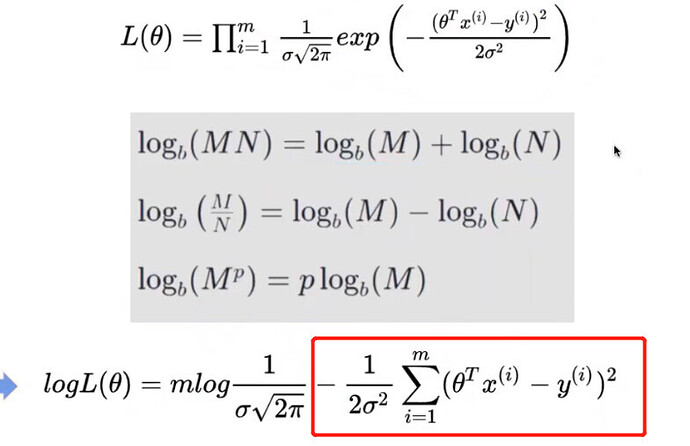如何理解最大似然估计方法的物理意义

数据科学
#1

想问下讲课的时候说的最大似然估计参数的方法，老师讲到使用特定参数使得曲线最符合频率分布直方图形状时还是可以理解的，但是接下来就转换成概率最大这部分不太理解。。
Q1: 概率最大说的是什么对于什么的概率最大？这个由概念到数学的转换是怎么做到的？应该怎么理解？
Q2: 最大似然估计方程L(θ) 是把所有点在given 对应行的x 的概率乘起来，这和最大似然估计的概念本身有什么联系？
Q3: 带入linear regression 公式到L(θ)之后取log，底数是多少？

image
image784×507 47.7 KB

这里需要详细的推导TAT

#2

  1. log底数可以是任意的（就差一个常数），为了方便这里可以取自然数e，也就是公式里的exp。先看单个的L， 取了log之后，就是logL = log[a * exp(b)], a就是exp前面，b就是exp后面，根据公式1，log(M * N) = logM + logN，所以logL = loga +log(exp(b))，后一项根据公式3， 把指数b放到前面去，即log(exp(b)) = b*log(e), 因为是自然数为底数，log(e) = 1， 所以单个logL= loga + b。再看整个L，因为是连乘，取log后 = log(L1 * L2 * L3…) = logL1 + logL2 + logL3 +…一共m个，把a和b的具体形式代入，整理一下就得到了最后的表达式。

  2. 最大似然估计中的数学表达式中，一方面，我们根据probabilistic assumption给出了数据的分布，它是关于x,y,theta的函数，物理意义是一个联合概率，表示多个(相互独立的)事件发生的联合概率。另一方面，我们当前观测到了诸多的(x,y)，那么如果把这些(x,y)带入上面的数据分布表达式中，表达的意思就是：我们观测到的这些数据在现实中出现的概率。这个概率当然是越大越好，因为它已经在现实中出现了。我们需要做的，就是找到theta, 让这个概率尽可能地大。

#3

不太明白，观测到的数据不就是已经在现实中出现了吗？那不就是概率=1 吗？

还有个问题是，在linear regression推论里，噪声服从正态分布怎么得出 given x, y就服从一样的正态分布呢？在几何意义上怎么理解呢？

y(true) = wx+b+epsilon, 当讨论y|x的时候，是由于每个x值相同的点对应到公式上是epsilon不一样导致最后y值不一样的吗？

老师在回复中写“多个相互独立事件发生的联合概率”，在这里多个相互独立事件指的是观测数据在现实中出现的概率，观测数据是哪些？哪些是在现实中出现的？既然观测数据就是在现实中出现的了，那所谓概率是谁相对于谁的概率？和我们的表达式又有什么关系？

连乘这个操作，把x相等的点也互相都乘进去了，意思是我们看概率是一个点一个点看的吗？

比如我有观测到（0，1）（0，2）（0，1）（0，2）（0，2）（0，3）（0，4）（1，4）（3，4），然后用y=wx+b+epsilon进行参数估计，老师可以用这个例子把整个过程讲一遍吗？现在都是数学公式太抽象了

课上讲最大似然估计法后直接引入wx+b+epsilon表达式了，好像跟squared loss没有什么关系，是不是只是最后写公式发现其中有一部分刚好是squared loss function？为什么不直接求squared loss 的最小值呢？

#4
  1. y=wx+b+noise, 如果x确定的话，那么(wx+b)这一项就是常数了，因此y|x的随机性完全来自于noise, 也就是说 y|x的分布于noise的分布完全一样。
  2. 你的理解是对的。
  3. &4.&5. 注意：在统计机器学习中，我们本质上在解的是overdetermined equation, 直观来理解就是，事件的发生是具有随机性的。比如，对于固定的一个x, 多次对它做观测，可能得到很多个不同的y (e.g., y1, y2, y3, …)。因此不能说"因为y1出现了，所以y1|x出现的概率就是1"，因为这次出现的y1可能是偶然事件。当然，如果多次观测看到的y都是一样的，都是y1, 那么y1|x的概率就很高了，但是我们还是无法保证它的概率一定是1。对于MLE，我们看的是所有这些observation整体出现的概率最大，意思是一样的。
  4. 这个问题exactly是咱们在课上反复讲的"用MLE推导linear regression loss function的结论与least squared loss结果一致"的内容，你可以看一下class 4 section 1.3的讲义。对于你的问题”为什么不直接求squared loss 的最小值呢？“，简单来说，直接求squared loss最小值，与用MLE得到最后的loss function结果，含义完全一样，只不过是同一个结论的两种不同的给出方法。
#5

谢谢老师，有几个follow up：

目前理解了您说的【不能说"因为y1出现了，所以y1|x出现的概率就是1"，因为这次出现的y1可能是偶然事件】。

  1. 那我们用联合概率密度函数，把所有观测到的点带入概率密度函数后相乘取最大，求出的θ的几何意义是什么呢？是把所有x相同的观测点 集中在了以y值为横坐标的钟型曲线上？
  2. 把每个点带入概率密度函数都可以求一出θ的解，这个的意义相当于让这每个点都出现在穿过这个点的钟型曲线上。那这些θ的意义是什么？
  3. 把每个点带入概率密度函数然后相乘怎么理解呢？因为我们说1）概率密度函数的每个点都不代表概率，而且，2）就算把这个点带进去，也不见得这个点一定落在钟型曲线的最大值上，因此相乘求最大也不能代表概率最大
  4. 把概率密度函数相乘又怎么理解呢？函数和函数相乘，怎么就相当于让整体observation出现的概率最大呢？函数相乘在几何意义上如何理解呢？
#6

这些观测到的点(xi, yi), 有一些点的x一样， 有一些点的x不同。如果正巧所有观测的x都是一样的， 那么就是given这个x对应的就是一个钟形曲线，如果有一些不同的x, 那么它们对应的y|x的钟形曲线不是同一个，至少mean不一样，但是由于他们相互独立，整体上都可以连乘起来。因此可以理解为，很多钟型函数连乘起来得到的这个联合概率密度函数，我们不知道它的形状具体是什么，但这无所谓，因为我们只要让它在所有观测点整体(xi, yi)上的概率最大就可以了。这个θ的物理意义就是来自于最大似然估计(MLE)的定义，θ所决定的这个distribution, 与观测到的distribution的matchness最大 （注意，强调一下，这个联合概率密度函数对应的曲线， 不一定是钟型的，我们不知道它的形状）。我是用联合概率来定义这个matchness的。函数相乘没有更多可以直观理解的几何意义。

#7

求老师对应回答一下这几个follow up~

  1. 如果有10个点，其中5个点的x一样，那这五个钟型曲线也一样，这要乘五次吗？还是五个点只乘一次？
  2. 联合概率密度函数取最大解得θ，相当于这个θ让每个点都位于穿过它的钟型曲线的最高点？可以这么理解吗？
  3. 如果X都一样，也是多个钟型曲线相乘，也不是钟型吧？
  4. 概率密度函数不是说纵轴不表示概率吗？那相乘出的联合概率密度函数是不是也不表示概率？
  5. 联合概率最大、matchness最大这些都不直观，对于“最大”这个表达到底是相对于谁最大，是指目前观测到的这些点 相对于无数个其他点，出现的概率最大吗？
#8

你说得对。根据联合概率的表达式，五个点就是乘5次，因此即使xi都一样，多个钟形曲线相乘也不是钟型。最优解θ的意义，可以认为是让整体联合概率取最大值，但是不一定让每一个点都取最大，可能是有些很大，有些比较小，但整体连乘后的结果取最大值，这就足够了。

问题4这个事情我们在课上也讲过多次，纵轴确实是概率密度，要算概率的话需要积分，但是积分的x轴范围是确定的，因此算不算积分都无所谓了，可以直接求概率密度的最大值就可以了。这个最大的含义请看课件上的严格英文解释，表示的是在某个theta取值下，由分布假设所描述的“已被观测到的事件”的出现概率最大。