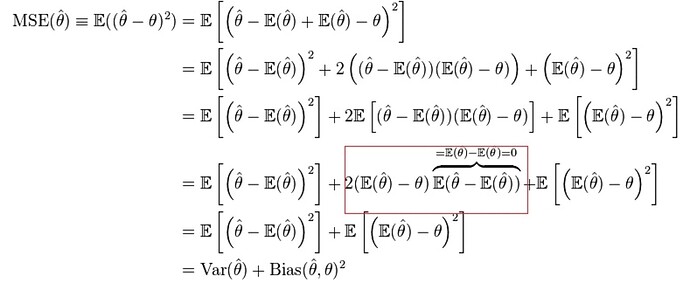汪老师,您在model bias & variance录播课里讲说model bias = E(\hat{f}) - y,但是我看一些textbook里面对于bias的定义是 E(\hat{f}) - f,并不是E(\hat{f}) 和observation y 的差值。请问这两个定义有什么区别吗?
你说的是对的。我们在课件里中做了一些简化。严格来说,在bias & variance公式中,对dependent variable三种表示:
- \hat{f} 表示 trained model (based on certain training data D);
- f 表示true model
- y 表示observation. y = f + \epsilon. E(\epsilon) = 0
严格来说, model bias = E(\hat{f}) - f. 也就是我们说的 “Model space中多个模型的平均输出结果与真实值相比的差距”, 这里说的真实值就是true model, 不应该是observation. 因为某一个observation也是包含噪声的,而true model 相当于从期望层面剔除了噪声的影响。
在我们的课件中,我们没有提 “true model f”的概念,而是用observation y替代了true model。这样做不影响大家直观理解bias & variance的概念,但是在数学上是有不严谨的地方的。考虑到面试和工作中不会要求相关数学推导,更多的是直观理解(比如我们课上讲的画图和例题),因此我们就选择少引入一个数学表达。谢谢你提出这个问题!
谢谢老师!所以如果y代表的是true model, 那么我们用squared error的话,irreducible error部分是如何没有的呢?
恩当我们用squared error的时候,通过数学推导(咱们这节课的Page 16讲了最后结论) 可以证明,expected squared error 直接等于bias ^ 2 + variance. noise这一项正好被消掉了。这是squared error的性质。在推导过程中,正如你所说,最好还是应该把 bias的定义写为,E(\hat{f}) - f,这样更清楚。我们在课件里还是用y替代了f. 如果你需要看具体推导过程的话,我可以之后在techie论坛上安装一个latex插件,然后在下方把具体推导过程写一下。由于这一般不会在面试中出现,我就不在课上和大家讲了 
好的,谢谢老师!
汪老师,在课件里的公式squared bias 是(\bar{f(x)} - y)^2,请问那个\bar{f(x)}就是E(\hat{f(x)}) 对么?还有那个 f(x;D) 是predicted value on training data D 是么,谢谢!
是的. \bar{f(x)} 严格写的话就是 E(\hat{f(x)}), 注意这里的Expectation是相对于model space D而言的,更严格地写是 E_D(\hat{f(x)}). f(x;D) 就是predicted value on training data D, 这里严格来说其实应该是 \hat{f(x;D)}, 因为它是预测值,并不是观测到的值。
汪老师,我比较好奇irreducible error 在squared error的情况下是如何cancel out的。我学的error decomposition 是这种
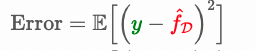
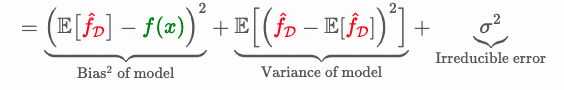
如果把bias里面的f(x)写成y-\epsilon 的形式,貌似也得不到课件里那个没有noise的公式。想请教下课件里的公式推导。谢谢!